今日热播
播放
下一个
打开循环播放
00:00
/
00:00
你可以 刷新 试试
播放信息
上传日志
视频ID
VID
j3167qm1a6q
播放流水
Flowid
af9ad736f686338bf774a2865e3e630b
播放内核
Kernel
-
显示器信息
Res
-
帧数
-
缓冲健康度
-
网络活动
net
-
视频分辨率
-
编码
Codec
-
mystery
mystery
-
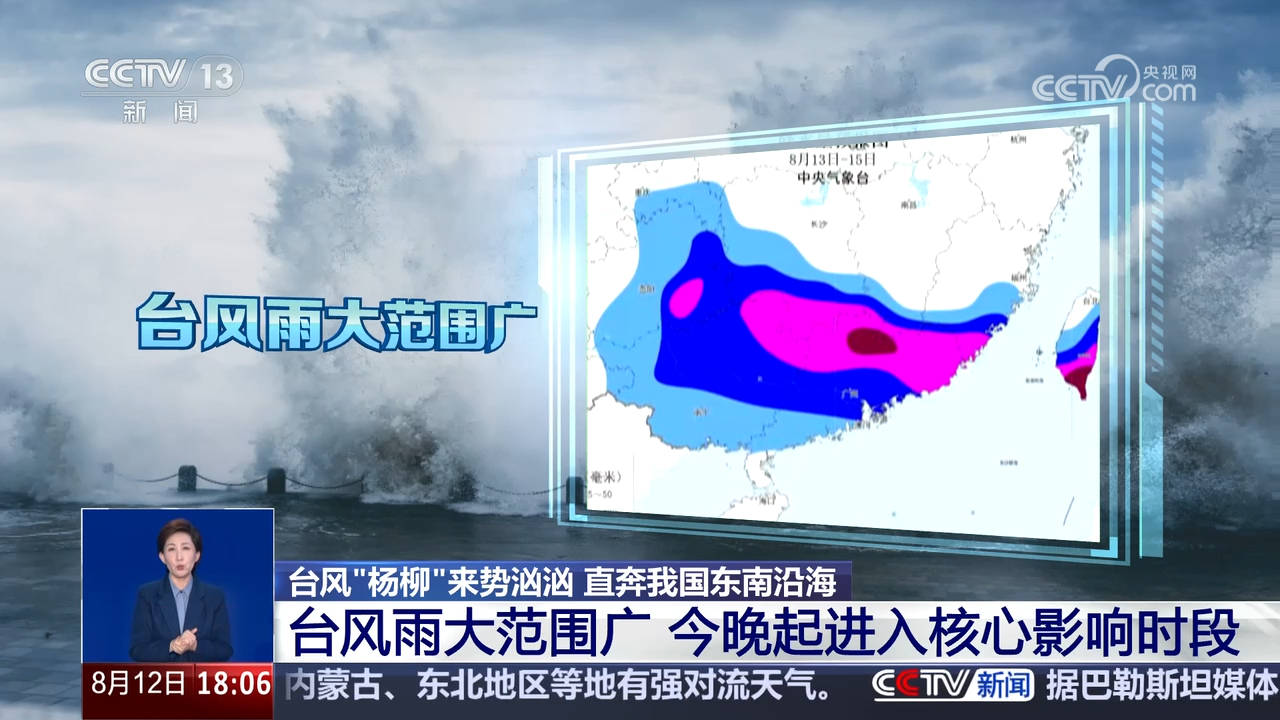
台风“杨柳”来势汹汹 直奔我国东南沿海
台风“杨柳”来势汹汹 直奔我国东南沿海
米价持续上涨 韩国首推“稻谷借贷”制度
米价持续上涨 韩国首推“稻谷借贷”制度
俄乌在顿涅茨克一军事重镇方向持续争夺
俄乌在顿涅茨克一军事重镇方向持续争夺
大湾区机器人产业有什么优势?他们一致回答“供应链”!
大湾区机器人产业有什么优势?他们一致回答“供应链”!